METODE KARNAUGH MAP

 1. Apa itu Metode Karnaugh Map

Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.

Karnaugh Map Method (metode peta Karnaugh ) adalah metode untuk menyederhanakan persamaan aljabar Boolean. Metode ini pertama kali diperkenalkan oleh Maurice Karnaugh pada tahun 1953 yang merupakan penyederhanaan dari metode Veitch Chart (Kartu Veitch).

Rumus untuk menentukan jumlah kotak pada K-Map adalah 2^n yang mana n adalah banyaknya variabel / inputan.

Langkah – langkah pemetaan K-Map secara umum :

1. Menyusun aljabar boolean
2. Menggambar rangkaian digital
3. Membuat tabel kebenaran
4. Merumuskan tabel kebenaran nya
5. Lalu merumuskan tabel kebenaran ke K-Map 

Jenis-Jenis K-Map

1.  K-Map 2 Variabel
2.  K-Map 3 Variabel
3. K-Map 4 Variabel
4. K-Map 5 Variabel
5. K-Map 6 Variabel

2. Tahap-tahap Penyelesaian Metode  Karnaugh Map

Langkah-langkah menggunakan metode peta Karnaugh  adalah sebagai berikut:

1. Pastikan terlebih dahulu persamaan Boolen berada dalam bentuk standar. Dalam hal ini saya menggunakan standar SOP (Sum Of Product).

Contoh :

2. Susun tabel kebenaran untuk persamaan di atas

3. Buat peta Karnaugh dengan jumlah kotak 2n dengan n = banyaknya variabel. Dari contoh di atas, terdapat 3 variabel sehingga kotak peta Karnaugh adalah 23 = 8 kotak. Dan masukkan minterm (m) dari tabel kebenaran ke dalam kotak yang sesuai.

4. Buat loop atau kelompok pada minterm-minterm yang berdekatan dengan banyaknya anggota kelompok 1, 2, 4, 8 atau 16 supaya dapat dihilangkan minterm yang berlawanan.

Pada tabel Karnaugh di atas terdapat kelompok dengan 2 anggotam minterm yaitu kelompok biru dan kelompok merah. Masing-masing kelompok beranggotakan 2 minterm. Maka persamaan minimum dapat diperoleh dari gabungan minterm yang ada pada tiap-tiap kelompok yaitu :

5. Tulis ulang bentuk minimum dari persamaan aljabar Boolean yaitu :

6. Buat rangkaian digital dengan menggunakan persamaan minumum pada no 5

3. Contoh soal Dan Penyelesaian Metode Karnaugh Map

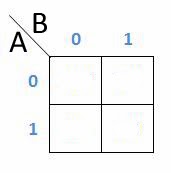
Penyederhanaan 2 Variabel

Catatan : Bar = ‘

Tabel dari K-Map 2 variabel adalah seperti dibawah ini

Contoh Soal :

H = AB + A’B+AB’

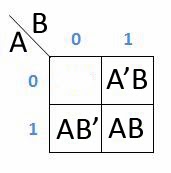
Maka cara pengerjaanya seperti dibawah ini

Bar (‘) atau aksen biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar aksen.

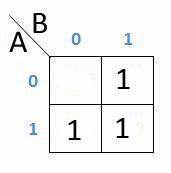
Dan dapat dipermudah lagi menjadi dibawah ini :

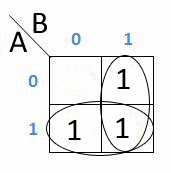
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya:

Karena kolom ber angka 1 dan baris ber angka 1 memenuhi setiap garisnya, maka dapat disimpulkan kalau H = AB + A’B+AB’ K-Map nya adalah AB/BA

Penyederhanaan 3 Variabel

Catatan : Bar = ‘

Tabel dari K-Map 3 variabel adalah seperti dibawah ini

Contoh Soal

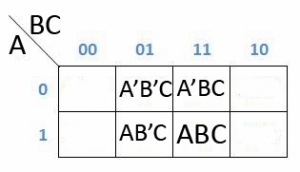
H = ABC + A’BC+A’B’C+AB’C

Maka cara pengerjaanya seperti dibawah ini

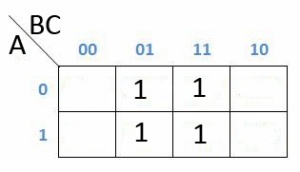
Dan dapat dipermudah lagi menjadi dibawah ini

Sekarang kita lihat, karena yang memenuhi setiap kotaknya adalah baris 01 dan 11 sedangkan simbol 01 artinya adalah (B’C) dan 11 artinya adalah (BC) dan simbol yang tidak ada aksen nya hanya C, maka H = ABC + A’BC+A’B’C+AB’C adalah C.

Penyederhanaan 4 Variabel

Catatan : Bar = ‘

Tabel dari K-Map 4 variabel adalah seperti dibawah ini :

Contoh Soal

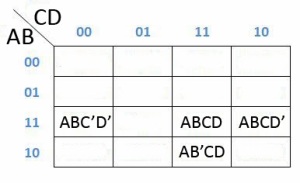
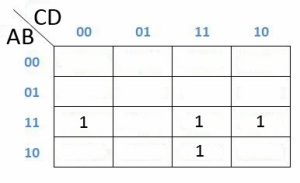
H = ABCD + ABCD’+AB’CD+ABC’D’

Maka cara pengerjaanya seperti dibawah ini

Dan dapat dipermudah lagi menjadi dibawah ini :

Karena yang ada angka 1 nya ada di kolom dan baris 1100, 1111, 1110 dan 1011, yaitu AB, ABCD, ABC dan ACD maka jika kita eliminasi dengan cara mengambil huruf yang sama saja menjadi AB + ABC + ACD.

Penyederhanaan 5 Variabel

Sedikit berbeda dengan Peta Karnaugh 2, 3 dan 4 variabel, peta Karnaugh 5  variabel, kita menggambar daerah kuadran. Peta Karnaugh dengan 5 variabel memiliki 2 daerah kudran dan  Perhatikan contoh:

Gambar Peta Karnaugh 5 variabel

Versi hamparan peta Karnaugh, yang ditunjukkan di atas, hanyalah dua (empat untuk peta 6-variabel) yang identik kecuali untuk bit paling signifikan dari alamat 3-bit di bagian atas.

Jika kita melihat di bagian atas peta, kita akan melihat bahwa penomoran berbeda dari peta kode Gray sebelumnya. Jika kita mengabaikan digit paling signifikan dari angka 3-digit, urutan 00, 01, 11, 10 ada di heading dari kedua sub peta.

Mari kita gunakan Peta Karnaugh 5-variabel untuk digunakan. Rancang sirkuit yang memiliki input biner 5-bit (A, B, C, D, E), dengan A menjadi MSB (Bit Paling Signifikan). Ini harus menghasilkan logika keluaran High untuk setiap bilangan prima yang terdeteksi dalam data masukan.